Rendering Julia set fractals

Published: at 12:00 AMSuggest Changes

The Julia set, named after the french mathematician Gaston Julia, represents a complex pattern generated by iterating the function f(z)=z2+cf(z) = z^2 + c on complex numbers. Each point in the complex plane is tested by repeatedly applying this function, with its behavior revealing whether it “escapes” to infinity or stays bounded. The resulting set of points that remain bounded forms intricate, self-similar shapes that vary depending on the value of cc.

In this article, we’ll explore how to efficiently render the Julia set fractals on the CPU and implement a smooth, asynchronous zooming effect.

Link to source code on Github : source code

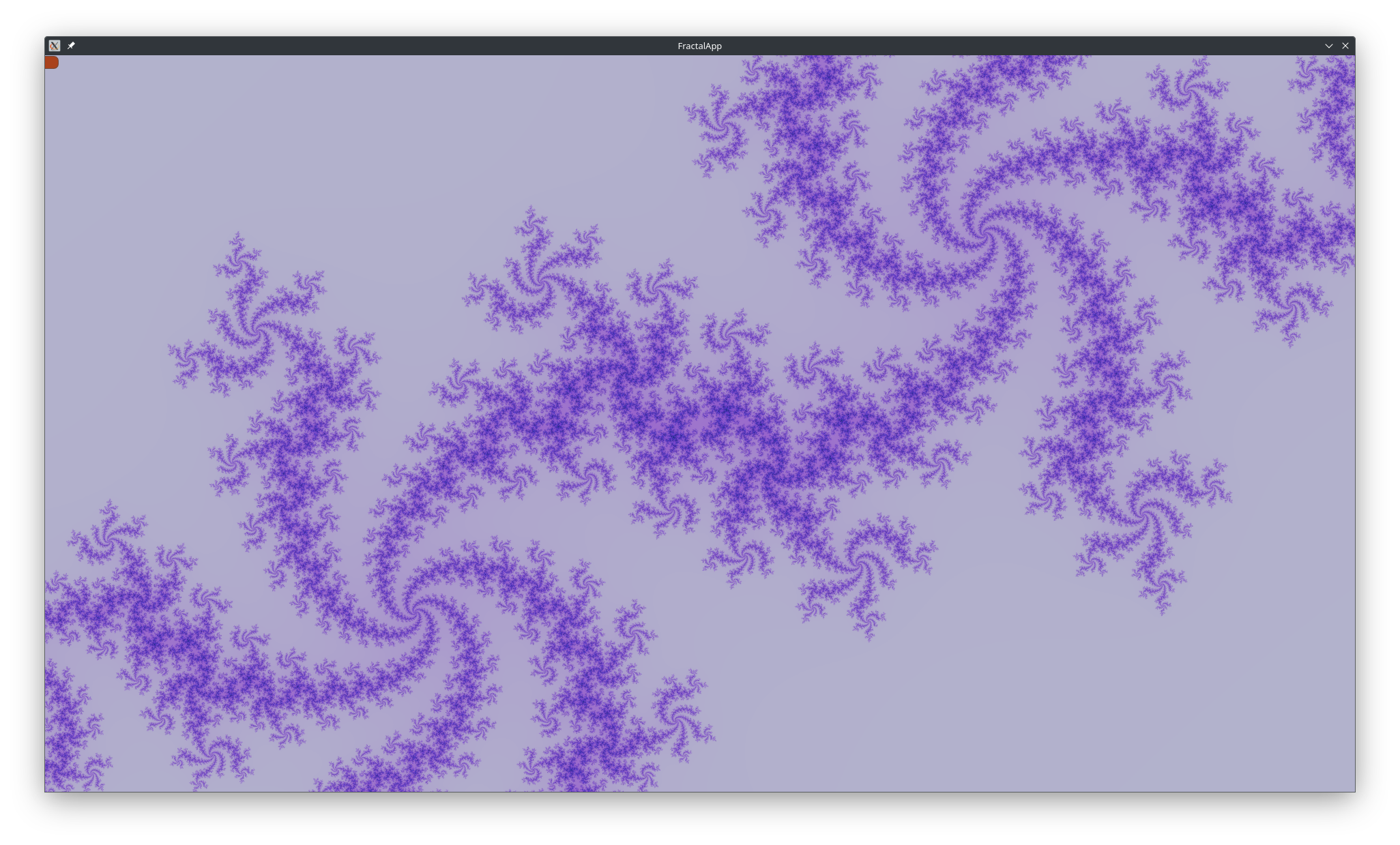
Table of contents

Open Table of contents

Why we will avoid the GPU

GLSL shaders are programs that run directly on the graphics card, making them an ideal choice for rendering fractals due to their parallel processing power. However, they come with a significant limitation: GLSL shaders support only single-precision floating-point arithmetic. When zooming deeply, the reduced precision can lead to visible artifacts and loss of detail at relatively shallow zoom levels.

Here is an example you can try in Shadertoy.

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec2 resolution = iResolution.xy;
    vec2 center = vec2(0.0, 0.0); 
    float scale = 100000.0;  
    int maxIterations = 1000;
    vec2 scaledCoord = (fragCoord - resolution * 0.5) / scale + center;
    vec2 c = vec2(-0.7269, 0.1889);  
    vec2 z = scaledCoord;
    int iterations;
    for (iterations = 0; iterations < maxIterations; iterations++) {
        if (dot(z, z) > 4.0) break;
        z = vec2(z.x * z.x - z.y * z.y, 2.0 * z.x * z.y) + c;
    }
    float color = float(iterations) / float(maxIterations);
    fragColor = vec4(vec3(color), 1.0);
}

We see that we lose details at a scale of 1e5:

CPU Julia iterations

In this section, we will focus solely on the function that takes in coordinates on the complex plane and produces the number of iterations for the Julia set calculation.

Naive implementation

We will begin with a straightforward implementation of the Julia set formula f(z)=z2+cf(z) = z^2 + c. In this basic version, we directly compute the complex number multiplication and addition operations as needed.

int computeJulia(double px, double py, double cx, double cy, 
                    double escapeRadiusSquared, int maxIterations) {
    double x = px;
    double y = py;
    int iterations = 0;
    
    while (iterations < maxIterations) {
        double magnitudeSquared = x*x + y*y;
        if (magnitudeSquared > escapeRadiusSquared) {
            break;
        }
        
        double newX = x*x - y*y + cx;
        double newY = 2*x*y + cy;
        
        x = newX;
        y = newY;
        iterations++;
    }
    
    return iterations;
}

Rearranging calculations

To optimize the computation, we can reduce the number of multiplications by pre-calculating common terms. The second version stores the squares x2x^2 and y2y^2 at the start of each iteration. These values are then reused in both the escape condition check and the next position calculation. While mathematically equivalent to the first version, this arrangement can provide noticeable performance improvements.

int computeJulia(double px, double py, double cx, double cy, 
                    double escapeRadiusSquared, int maxIterations) {
    double x = px;
    double y = py;
    int iterations = 0;
    
    while (iterations < maxIterations) {
        double x2 = x*x;
        double y2 = y*y;
        double xy = x*y;
        
        double magnitudeSquared = x2 + y2;
        if (magnitudeSquared > escapeRadiusSquared) {
            break;
        }
        
        x = x2 - y2 + cx;
        y = 2*xy + cy;
        
        iterations++;
    }
    
    return iterations;
}

Using AVX2 intrinsics

To achieve further performance gains, we leverage AVX2 SIMD instructions. This vectorized implementation processes four points simultaneously using 256-bit wide vectors __m256d. The escape condition is checked using a vector comparison _mm256_cmp_pd, creating a mask that’s used to selectively increment iteration counts only for points that haven’t escaped.

__m256i computeJulia(__m256d positionX, __m256d positionY, __m256d constantX,
                     __m256d constantY, __m256d escapeRadiusSquared,
                     int maxIterations) {
  __m256d x = positionX;
  __m256d y = positionY;
  __m256i iterations = _mm256_setzero_si256();
  __m256i ones = _mm256_set1_epi64x(1);
  for (int i = 0; i < maxIterations; ++i) {
    __m256d x2 = _mm256_mul_pd(x, x);
    __m256d y2 = _mm256_mul_pd(y, y);
    __m256d mag2 = _mm256_add_pd(x2, y2);
    __m256d mask = _mm256_cmp_pd(mag2, escapeRadiusSquared, _CMP_LT_OQ);
    if (_mm256_movemask_pd(mask) == 0)
      break;
    __m256d xy = _mm256_mul_pd(x, y);
    __m256d newX = _mm256_add_pd(_mm256_sub_pd(x2, y2), constantX);
    y = _mm256_add_pd(_mm256_add_pd(xy, xy), constantY);
    x = newX;
    iterations = _mm256_add_epi64(
        iterations, _mm256_and_si256(ones, _mm256_castpd_si256(mask)));
  }

  return iterations;
}

Rendering to the screen

Mapping screen coordinates to the complex plane

To visualize the Julia set, we map screen coordinates (x,y)(x, y) to complex plane coordinates (a,b)(a, b) using three main steps: centering, scaling, and offsetting.

Centering shifts the screen origin from the top-left corner to the center, allowing symmetry around the middle.

Scaling, controlled by a factor ss, lets us zoom in and out on the fractal, while maintaining the aspect ratio by normalizing xx and yy relative to the screen’s width.

Offsetting by (x0,y0)(x_0, y_0) repositions the center of the screen to a specific point on the complex plane, enabling exploration of different regions of the fractal.

a=x−W2s⋅W2+x0a = \frac{x - \frac{W}{2}}{s \cdot \frac{W}{2}} + x_0 b=y−H2s⋅W2+y0b = \frac{y - \frac{H}{2}}{s \cdot \frac{W}{2}} + y_0

Color mapping with a LUT

Coloring is done using a Look-Up Table (LUT), which provides a fast way to map iteration counts to colors. The generatePalette function interpolates between base colors, creating a smooth gradient based on max iterations. Using a LUT eliminates the need to recompute colors repeatedly.

std::vector<ci::Color> generatePalette(const std::vector<ci::Color> &baseColors,
                                       int maxIterations) {
  std::vector<ci::Color> palette(maxIterations + 1);
  palette[maxIterations] = ci::Color(0.1f, 0.1f, 0.3f);
  for (int i = 0; i < maxIterations; i++) {
    float t = (float)i / maxIterations;
    t = t * (baseColors.size() - 1);
    int idx = static_cast<int>(t);
    float fract = t - idx;
    const ci::Color &c1 = baseColors[idx];
    const ci::Color &c2 =
        baseColors[std::min(idx + 1, (int)baseColors.size() - 1)];
    palette[i] =
        ci::Color(ci::lerp(c1.r, c2.r, fract), ci::lerp(c1.g, c2.g, fract),
                  ci::lerp(c1.b, c2.b, fract));
  }

  return palette;
}

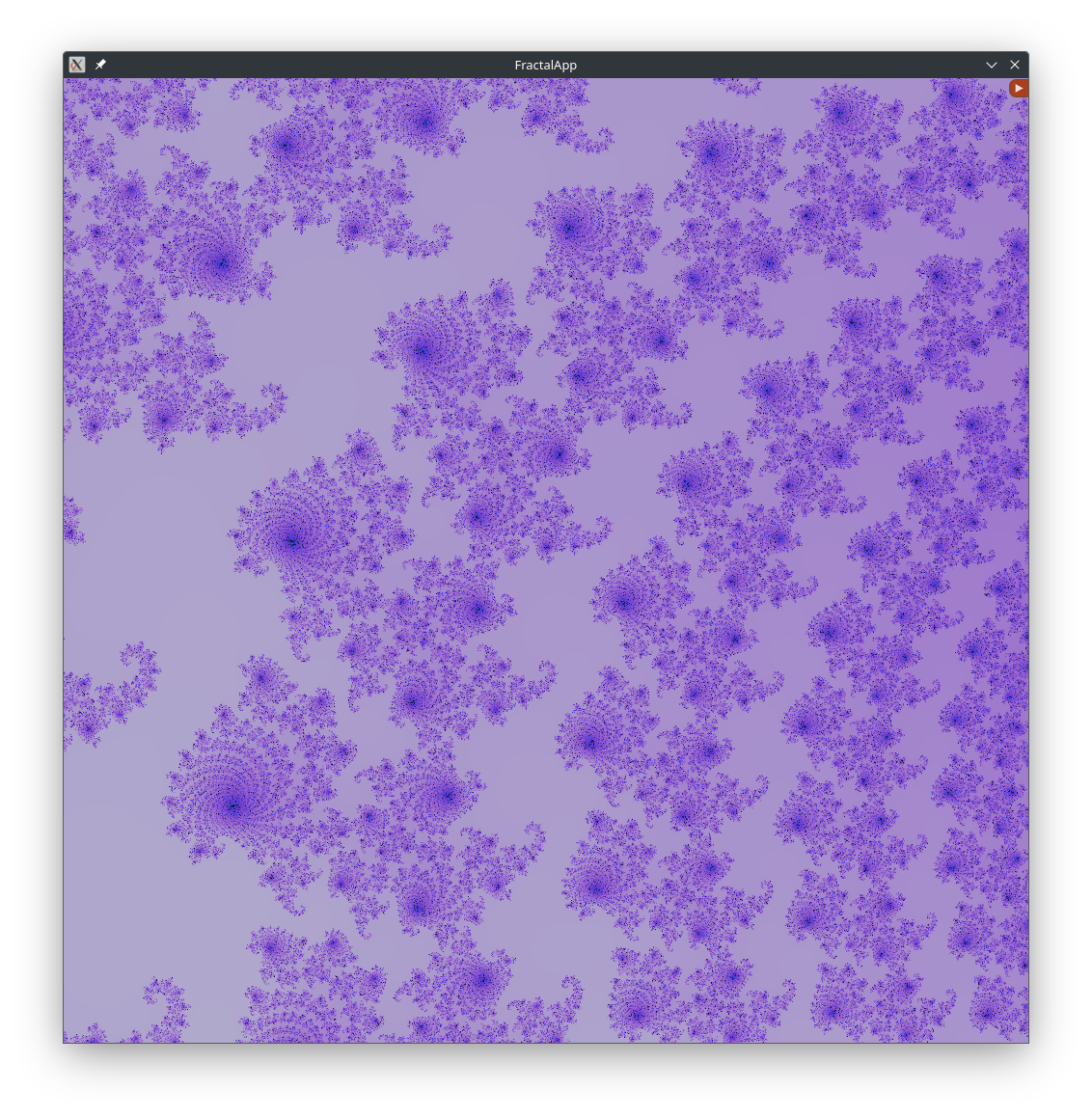
Enhancing image quality with supersampling

To improve image quality and reduce aliasing artifacts, supersampling is applied. In this approach, each pixel is divided into multiple sub-pixel samples, with coordinates slightly offset from the main pixel center. For each sub-sample, the Julia set function is evaluated, and the results are averaged to produce a smoother, higher-quality final color for the pixel.

Supersampling Count: 1Supersampling Count: 4

Putting it all together

Combining everything, the renderJulia function integrates coordinate transformations, supersampling, and color mapping to render the fractal with OpenMP parallelism onto the ci::Surface32f object:

void renderJulia(ci::Surface32f &surface, const RenderParameters &params,
                 const std::vector<ci::Color> &palette) {
  int surfaceWidth = surface.getWidth();
  int screenHeight = surface.getHeight();
  double surfaceWidthHalf = surfaceWidth / 2.0;
  double surfaceHeightHalf = screenHeight / 2.0;
  double scaleInv = 1.0 / params.scale;
  double totalSamples = params.samplingCount * params.samplingCount;
#pragma omp parallel for
  for (int y = 0; y < screenHeight; y += 1) {
    for (int x = 0; x < surfaceWidth; x += 4) {
      __m256d surfaceWidthHalfVec = _mm256_set1_pd(surfaceWidthHalf);
      __m256d scaleInvVec = _mm256_set1_pd(scaleInv);
      __m256d xVec = _mm256_set_pd(x + 3, x + 2, x + 1, x);
      __m256d xShifted = _mm256_sub_pd(xVec, surfaceWidthHalfVec);
      double accumulatedR[4] = {0}, accumulatedG[4] = {0};
      double accumulatedB[4] = {0}, accumulatedA[4] = {0};
      for (int sy = 0; sy < params.samplingCount; sy++) {
        for (int sx = 0; sx < params.samplingCount; sx++) {
          double subX = sx / static_cast<double>(params.samplingCount);
          double subY = sy / static_cast<double>(params.samplingCount);
          __m256d posX = _mm256_add_pd(
              _mm256_mul_pd(
                  _mm256_mul_pd(_mm256_add_pd(xShifted, _mm256_set1_pd(subX)),
                                scaleInvVec),
                  _mm256_set1_pd(1.0 / surfaceWidthHalf)),
              _mm256_set1_pd(params.offsetX));
          __m256d posY = _mm256_set1_pd((y + subY - surfaceHeightHalf) /
                                            surfaceWidthHalf * scaleInv +
                                        params.offsetY);
          __m256d constX = _mm256_set1_pd(params.constantX);
          __m256d constY = _mm256_set1_pd(params.constantY);
          __m256d escRadSq = _mm256_set1_pd(params.escapeRadiusSquared);
          __m256i iterations = computeJulia(posX, posY, constX, constY,
                                            escRadSq, params.maxIterations);
          int64_t iterCounts[4];
          _mm256_storeu_si256((__m256i *)iterCounts, iterations);
          for (int i = 0; i < 4; ++i) {
            if (x + i < surfaceWidth) {
              int idx = std::min(iterCounts[i],
                                 static_cast<int64_t>(params.maxIterations));
              ci::ColorA color = palette[idx];
              accumulatedR[i] += color.r;
              accumulatedG[i] += color.g;
              accumulatedB[i] += color.b;
              accumulatedA[i] += color.a;
            }
          }
        }
      }
      for (int i = 0; i < 4; ++i) {
        if (x + i < surfaceWidth) {
          ci::ColorA finalColor(
              accumulatedR[i] / totalSamples, accumulatedG[i] / totalSamples,
              accumulatedB[i] / totalSamples, accumulatedA[i] / totalSamples);
          surface.setPixel(ci::ivec2(x + i, y), finalColor);
        }
      }
    }
  }
}

User interactivity

Users can interact by holding and dragging the mouse to move the fractal around. Use the mouse wheel to zoom in or out, the arrow keys to pan, and the +/- keys to adjust the zoom level.

This is achieved using Cinder’s functionality provided by mouseDown, mouseDrag, mouseUp, mouseWheel, and keyDown events.

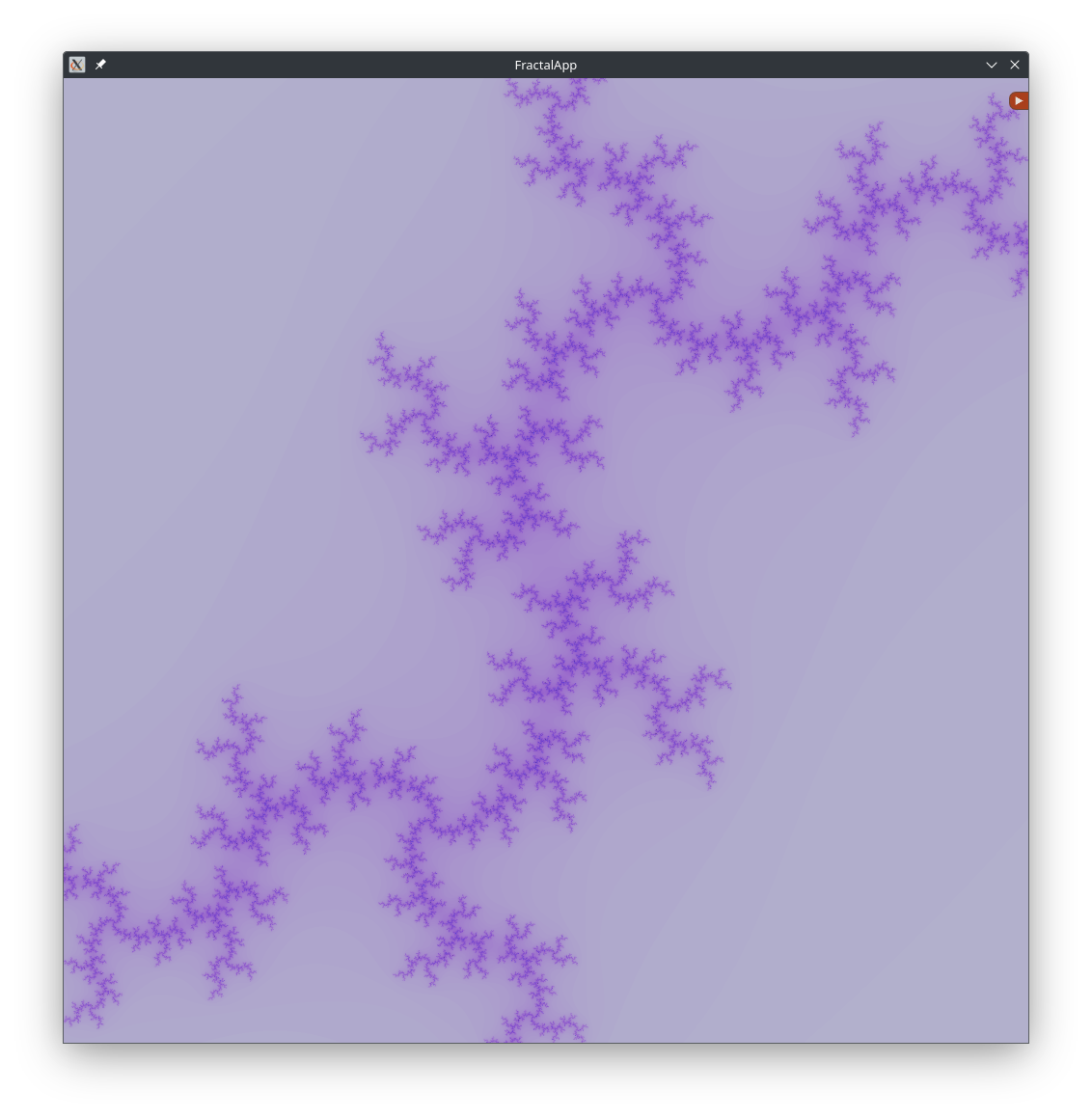
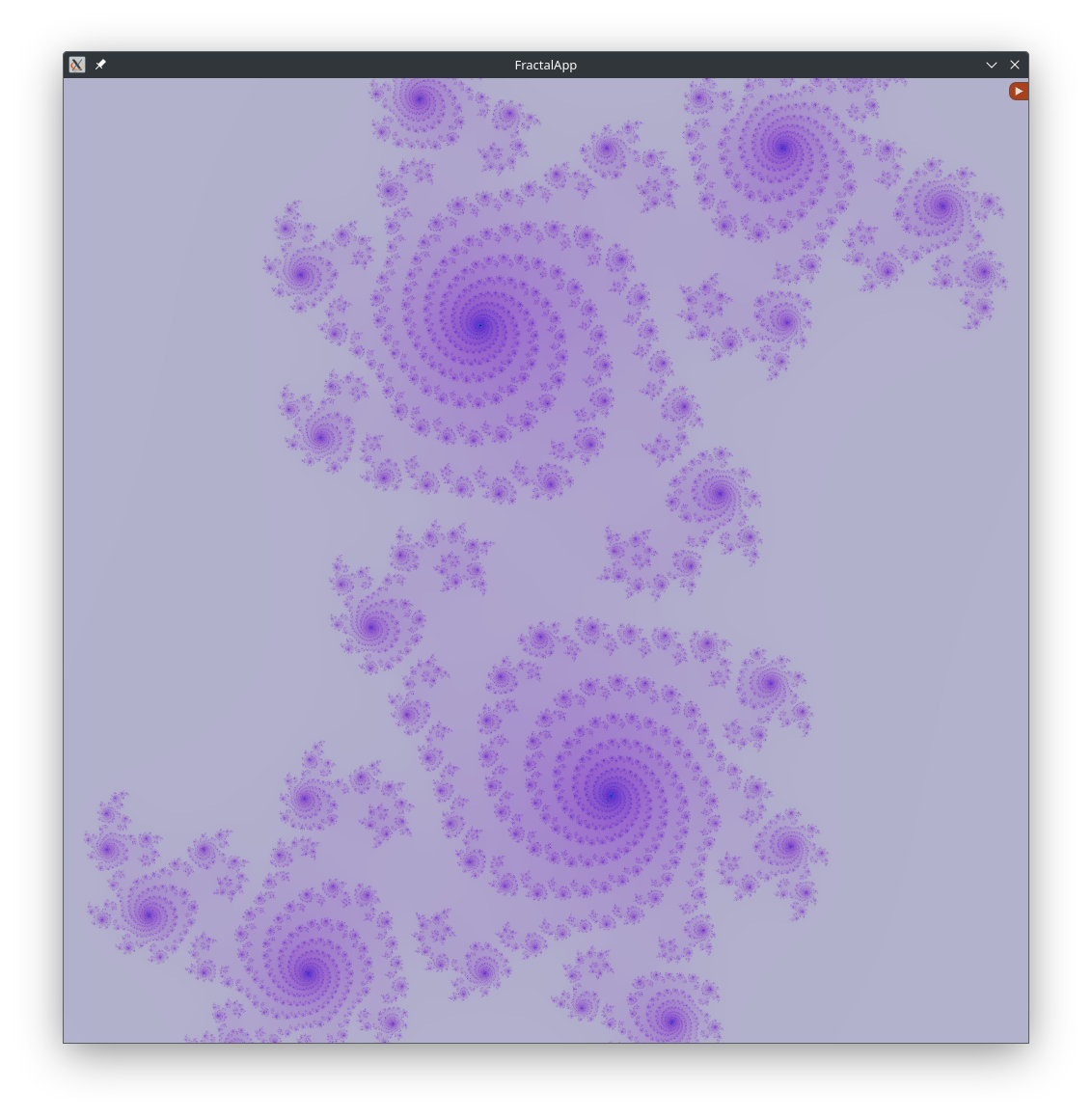
Results

Below are some renders with different constants:

Smooth Zooming with Asynchronous Rendering

We want to enable users to initiate a zooming animation that allows them to explore the mesmerizing details of the fractal. While we could simply render each frame with a new scale, doing so in real time would be too slow and cause stuttering. Instead, we will define an asynchronous renderer that handles the next zoomed frame in the background, while the app simulates the zoom by cropping and resizing the current image. Once the next frame is ready, it seamlessly swaps in, ensuring a smooth and responsive animation without putting excessive strain on performance.

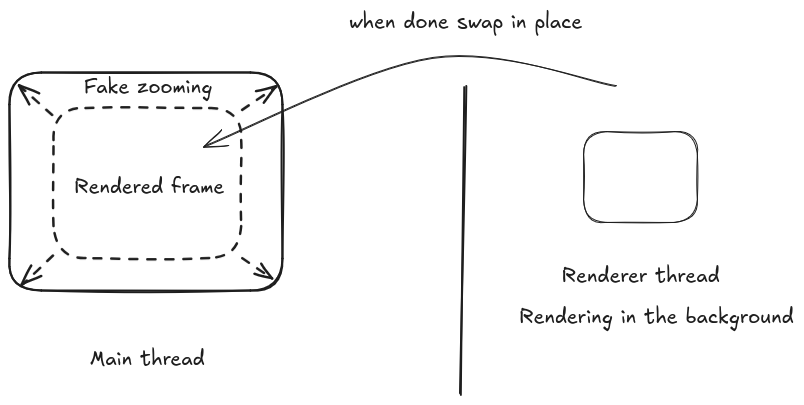
Renderer Class

The Renderer class manages rendering tasks in a multi-threaded environment. It uses a background thread (renderThread) to process rendering requests. Requests include a surface to render to, render parameters, a color palette, and an optional callback function. These requests are queued and processed asynchronously.

struct RenderRequest {
  ci::Surface32f &surface;
  const RenderParameters &params;
  const std::vector<ci::Color> &palette;
  const std::function<void()> callback;

  RenderRequest(ci::Surface32f &surf, const RenderParameters &p,
                const std::vector<ci::Color> &pal,
                const std::function<void()> cb)
      : surface(surf), params(p), palette(pal), callback(cb) {}
};

class Renderer {
public:
  Renderer() : running(true) {
    renderThread = std::thread(&Renderer::run, this);
  }

  ~Renderer() {
    {
      std::lock_guard<std::mutex> lock(mtx);
      running = false;
    }
    cv.notify_one();
    if (renderThread.joinable()) {
      renderThread.join();
    }
  }

  void requestRender(ci::Surface32f &surface, const RenderParameters &params,
                     const std::vector<ci::Color> &palette,
                     const std::function<void()> callback) {
    {
      std::lock_guard<std::mutex> lock(mtx);
      requests.emplace(surface, params, palette, callback);
    }
    cv.notify_one();
  }

private:
  std::thread renderThread;
  std::atomic<bool> running;
  std::queue<RenderRequest> requests;
  std::mutex mtx;
  std::condition_variable cv;

  void run() {
    while (true) {
      std::unique_lock<std::mutex> lock(mtx);
      cv.wait(lock, [this] { return !requests.empty() || !running; });
      if (!running && requests.empty()) {
        return;
      }
      if (!requests.empty()) {
        RenderRequest request = std::move(requests.front());
        requests.pop();
        lock.unlock();
        renderJulia(request.surface, request.params, request.palette);
        if (request.callback) {
          request.callback();
        }
      }
    }
  }
};

Results

The following zooming was made with constant −0.7269+1889i-0.7269 + 1889i

Next Post
Building an Autograd Library from Scratch in C for Simple Neural Networks